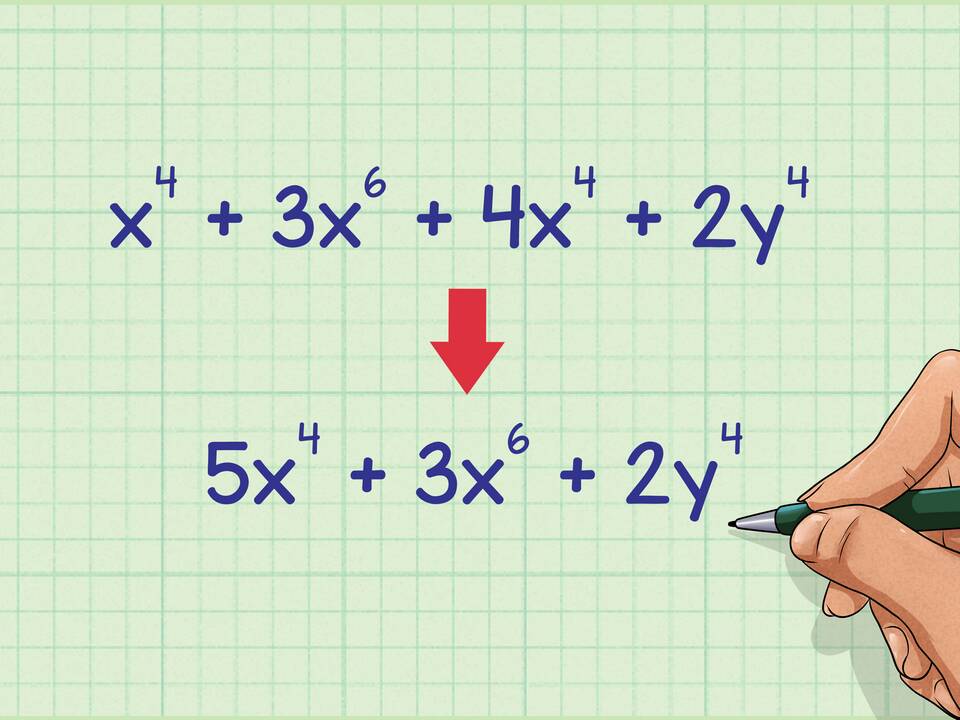Сумма степеней - это математическое понятие, которое встречается в различных разделах алгебры и теории чисел. Рассмотрим основные аспекты этого термина и его применение в математике.
Содержание
Основное определение
Сумма степеней представляет собой алгебраическое выражение вида an + bm + ... + zk, где a, b, ..., z - основания степеней, а n, m, ..., k - их показатели.
Виды сумм степеней
| Тип суммы | Пример | Описание |
| Однородная | x2 + y2 + z2 | Все степени имеют одинаковый показатель |
| Разнородная | a3 + b2 + c1 | Показатели степеней различны |
Применение сумм степеней
В алгебраических выражениях
- Разложение многочленов на множители
- Доказательство тождеств
- Решение уравнений высших степеней
В теории чисел
- Представление чисел в виде сумм степеней
- Исследование свойств простых чисел
- Решение диофантовых уравнений
Формулы для сумм степеней
Сумма квадратов
a2 + b2 = (a + b)2 - 2ab
Сумма кубов
a3 + b3 = (a + b)(a2 - ab + b2)
Обобщенная формула
Для натуральных n существует формула: an + bn = (a + b)(an-1 - an-2b + ... + bn-1) при нечетных n
Исторические примеры
| Случай | Формулировка |
| Гипотеза Эйлера | Для n > 2 сумма n степеней не может быть n степенью |
| Теорема Ферма | an + bn = cn не имеет решений в натуральных числах при n > 2 |
Заключение
Сумма степеней является важным математическим понятием с широким спектром применений. Понимание свойств и формул, связанных с суммами степеней, необходимо для решения сложных алгебраических задач и продвинутого математического анализа.