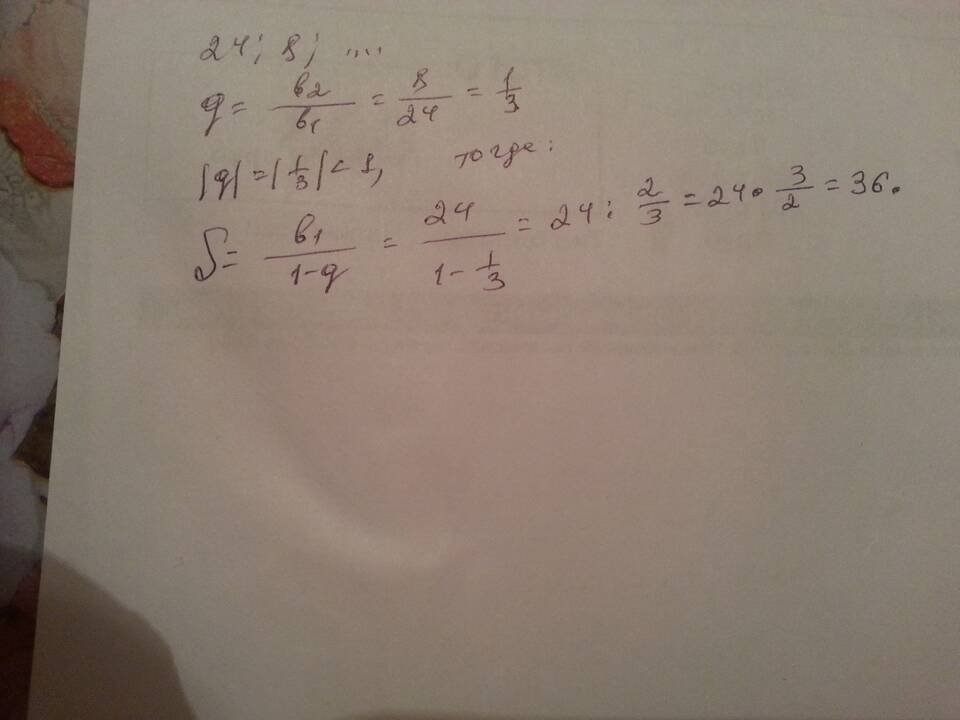Бесконечная геометрическая прогрессия представляет собой бесконечный ряд, составленный из членов геометрической последовательности. Рассмотрим условия сходимости и методы вычисления суммы такого ряда.
Содержание
Основные понятия
| Термин | Обозначение | Определение |
| Первый член | a₁ | Начальный элемент последовательности |
| Знаменатель | q | Отношение последующего члена к предыдущему |
| n-й член | aₙ | aₙ = a₁·qn-1 |
Условия сходимости ряда
- Ряд сходится, если |q| < 1
- Ряд расходится, если |q| ≥ 1
- При q = 1 ряд превращается в бесконечную сумму одинаковых слагаемых
- При q = -1 ряд колеблется между двумя значениями
Формула суммы бесконечной прогрессии
Сумма S бесконечно убывающей геометрической прогрессии вычисляется по формуле:
S = a₁ / (1 - q), где |q| < 1
Пошаговый алгоритм вычисления
- Определите первый член прогрессии a₁
- Вычислите знаменатель прогрессии q
- Проверьте условие сходимости |q| < 1
- Если условие выполняется, примените формулу суммы
- Если условие не выполняется, ряд расходится
Примеры вычисления суммы
| Прогрессия | Параметры | Сумма |
| 1 + 1/2 + 1/4 + 1/8 + ... | a₁=1, q=1/2 | S = 1/(1-1/2) = 2 |
| 3 - 1 + 1/3 - 1/9 + ... | a₁=3, q=-1/3 | S = 3/(1+1/3) = 9/4 |
Применение в математике
- Представление периодических десятичных дробей
- Решение задач теории вероятностей
- Вычисление пределов функций
- Анализ экономических моделей
Понимание метода вычисления суммы бесконечной геометрической прогрессии является важным инструментом в различных разделах математики и ее приложениях. Главное - правильно определить параметры прогрессии и проверить условие сходимости.