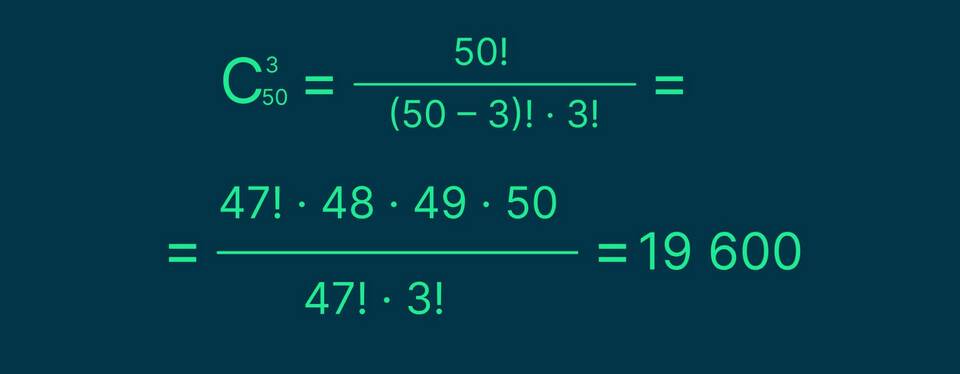| Тип суммы | Формула | Пример |
| Конечная сумма чисел | Σni=1ai | 1+2+3+...+n |
| Арифметическая прогрессия | Sn = n(a1+an)/2 | 2+5+8+...+29 |
| Геометрическая прогрессия | Sn = a1(1-rn)/(1-r) | 3+6+12+...+192 |
- Последовательное сложение всех членов
- Применяется для небольших последовательностей
- Пример: 1+2+3+4+5 = 15
- Определите тип последовательности
- Выберите соответствующую формулу
- Подставьте известные значения
- Выполните вычисления
| Шаг | Действие |
| 1 | Проверка базы (n=1) |
| 2 | Предположение для n=k |
| 3 | Доказательство для n=k+1 |
- Гармонический ряд: Σ1/n расходится
- Геометрический ряд: Σarn сходится при |r| < 1
- Признаки сравнения, Даламбера, Коши
| Метод | Применение | Пример |
| Частичных сумм | Sn = Σnk=1ak | Σ1/2k = 1 |
| Абеля | Для условно сходящихся рядов | Σ(-1)n/n |
| Чезаро | Среднее арифметическое частичных сумм | Ряд Гранди |
- Итеративный подход (циклы)
- Рекурсивное вычисление
- Использование формул (аналитическое решение)
- Параллельные вычисления
- Ошибка округления
- Потеря значимости
- Накопление ошибки
- Метод Кэхэна для точного суммирования
Практические рекомендации
- Для больших сумм используйте аналитические формулы
- Проверяйте сходимость бесконечных рядов
- Учитывайте погрешности при компьютерных расчетах
- Используйте специализированные математические пакеты
Решение суммы требует понимания природы последовательности и выбора оптимального метода. От простого арифметического сложения до сложных аналитических методов - правильный подход позволяет эффективно вычислять суммы любого типа.